« Full face mask and saltwater | Main | Altitude diving class at Meeks Bay, Lake Tahoe »
July 23, 2008
Diving at altitude revisited
As we've all been taught in Scuba class, the laws of messieurs Boyle and Dalton describe how air pressure and density, respectively, vary when we dive, and that of Mr. Henry how gasses get absorbed in liquids and tissues under pressure. Nitrogen absorption and release rates directly affect the no-decompression bottom times and are therefore extremely important to divers. The whole pressure picture changes at higher elevations because the air is thinner at altitude.
What we learn in Scuba class always assumes that the pressure at the surface is one atmosphere, or 14.7 pounds per square inch. Course materials then show how a certain volume of air is compressed to half at a depth of 33 feet because the additional pressure of the water on top of us adds another atmosphere, or 14.7 pounds per square inch, for a total of two atmospheres, or 29.4 pounds per square inch. At 66 feet the same volume of air is subjected to three atmospheres and has shrunk to one third of its original surface volume. Conversely, if you blow a certain amount of air into a balloon at a depth of 66 feet, that volume will double once you get back up to 33 feet, and triple at the surface. This is an essential part of understanding diving physics.
However, does this still hold true at altitude? Let's think this through with the example of Lake Tahoe, which is at 6,230 feet above sea level.
At first sight, it would seem that once you are fully acclimated to the Lake Tahoe altitude level, theoretical and actual depth should be the same. At Tahoe you start out at a surface air pressure of roughly 0.8 atmospheres. If you then dive down to 99 feet you'd add another atmosphere's worth of pressure each 33 feet, for a total of 3.8 atmospheres. Then you go back up to the surface where the pressure is once again 0.8 atmospheres. So the pressure difference betwen surface and 99 feet is three atmospheres. At sea level you'd go from 1.0 atmosphere at the surface to 4.0 atmospheres at a depth of 99 feet, and then back up to 1.0 atmospheres, for the same pressure difference of three atmospheres. If anything, when diving in Lake Tahoe you have less total pressure on top of you at 99 feet than at sea level (3.8 ata instead of 4.0 ata) where you'd reach 3.8 ata already at 93 feet. So why then do the altitude tables show that 99 feet at Tahoe corresponds to an ocean depth of about 125 feet and not 93?
The answer is that while the math in the above paragraph is correct, it does not address the problem we're trying to solve. The problem is the uptake of nitrogen, and that means we need to think in terms of pressure ratios and not pressure differences. At sea level, the pressure doubles at 33 feet compared to the surface, triples at 66 feet, and quadruples at 99 feet. Now look at Lake Tahoe where the surface pressure is only 0.8 atmospheres. That corresponds to 26.4 feet of water. So when you dive Lake Tahoe, the pressure doubles at 26.4 feet, triples at 52.8 feet, and quadruples at 79.2 feet. This means that as far as nitrogen ongassing and offgassing goes, you need to divide actual depth by surface pressure to arrive at theoretical depth.
That's because in Lake Tahoe, four times surface pressure is reached at 79.2 feet whereas at sea level four times surface pressure is reached at 99 feet. Henry's law says, "At a constant temperature, the amount of a given gas dissolved in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid." The way gasses dissolve and expand in liquids and tissues in the body is very complex, but if for simplicity's sake we assume that nitrogen bubbles expand as we ascend to the surface, those bubbles will expand to four times their size from a 79.2 feet dive in Lake Tahoe and from a 99 feet dive at sea level. That is why we need altitude conversion tables (click here for an example of such a chart.)
Below is a table that shows what I call "altitude nitrogen atmospheres." The colored lines show what depth surface pressure multiples correspond to at various altitudes. If you look at the purple line you see that as far as dive tables go, a 132 feet dive at sea level corresponds to a 110 feet dive at 5000 feet altitude and a 98 feet dive at 8000 feet altitude.
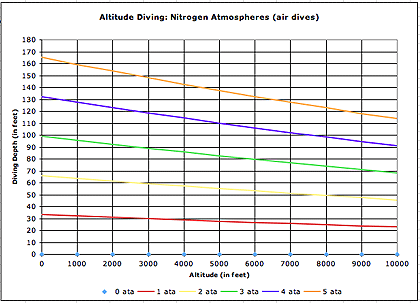
It should be obvious by now that altitude conversion tables are used to stay within safe decompression limits. So they handle the nitrogen side of things. But what about oxygen? That's an entirely different ballgame. As anyone who has taken an Enriched Air Diving, or Nitrox, class knows, high oxygen partial pressure can become a problem. Oxygen toxicity can occur when oxygen partial pressure exceeds certain values. This can lead to convulsions and loss of consciousness, and thus quite possibly drowning. The recommended oxygen partial pressure limit is 1.4 ata. The 1.4 ata limit is used by Nitrox divers to compute the "MOD," or "Maximum Operating Depth" of a Nitrox mix. The formula used to compute the MOD is:
MOD = (1.4 / oxygen percentage x 33 ) - surface pressure in feet of water.
If we dive EANx32 (32% Nitrox) at sea level, the MOD is 111.38 feet. But what would the MOD be if we dive 32% Nitrox at Lake Tahoe where the surface pressure is only about 0.8 ata? The answer is 118 feet! Yes, the MOD for diving EANx32 at that altitude is actually 6.4 feet deeper than at sea level. In fact, those 6.4 feet apply to all Nitrox percentages. That's because oxygen toxicity depends on pressure and not on pressure ratio.
That creates an interesting situation: As far as pressure goes, 99 feet in Tahoe is only as much as 93 feet in the ocean. But as far as nitrogen uptake goes those same 99 feet are like 125 in the ocean.
If we dive air, oxygen toxicity is rarely an issue. At Lake Tahoe levels, an air diver would not reach the 1.4 ata partial oxygen pressure level until a depth of almost 200 feet, far deeper than the recommended recreational diving depth limit. For Nitrox divers, however, the MOD can become an issue. At Lake Tahoe altitude, the MOD for a diver using 36% Nitrox is about 103 feet, and that is actual feet, not altitude adjusted feet.
The table below shows altitude-adjusted MOD levels for air as well as Nitrox with oxygen percentages between 30 and 40 percent. Again, the MOD at altitude gets deeper because the surface pressure, converted to the equivalent of feet of water, gets less and less.
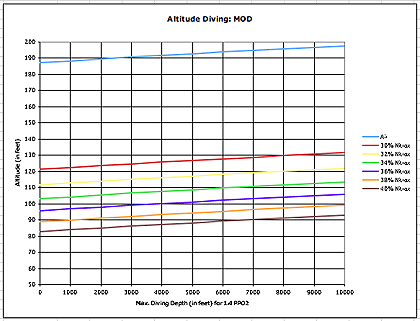
But what about altitude adjustment for Nitrox divers? Can they use the same altitude tables? Not directly. Nitrox divers know that in order to use regular dive tables, we need to first calculate the equivalent air depth, or EAD. The formula to compute EAD is:
EAD = (( Partial Pressure Nitrogen / 0.79 ) * (depth + 33 feet)) - 33 feet
You can generate Nitrox Equivalent Air Depth tables in a spreadsheet program with this formula, then use those values to generate a second table that shows Equivalent Air Depth for a given percentage Nitrox at a given altitude, and then use those twice adjusted depths to look up maximum no-decompression bottom times in standard dive tables. What you'll find is that using Nitrox at altitude almost cancels out the effect of altitude: At altitude the equivalent ocean depth is deeper than the actual depth as far as nitrogen goes. But with diving Nitrox the equivalent air depth is always shallower than the actual depth as far as nitrogen goes. Depending on the altitude, diving a certain mix of Nitrox means you can use the standard no-decompression sea level air tables. For diving Lake Tahoe, for example, using 34% Nitrox gives you about the same bottom times as diving air at sea level.
I should also mention that NAUI has plastic dive tables for EAN32 and EAN36 both for altitudes between 2,000 and 6,000 feet and 6,000 and 10,000 feet. The tables are based on the Reduced Gradient Bubble Model and show maximum dive times for the initial dive and a second dive. They are fairly basic and probably include a good deal of safety.
Finally, it's essentially all moot as no one is using dive tables anymore anyway. The dive computer does it all, and almost no one knows how theirs works. That's why I felt a need to figure out how it all fits together. It's still good to know these things. Thanks also to Brian at diverssupport.com for helping me understand all these concepts.
Disclaimer: Although I am fairly confident in my math and checked my findings and results against a number of authoritative sources I do not claim all of this is correct and no one should base their dive plans on what I wrote here.
Posted by conradb212 at July 23, 2008 4:01 PM








